What Is Geohashing? Everything You Need To Know

Have you ever wondered how your ride-sharing app finds riders only nearby instead of the entire city? How does this happen at an algorithmic level?

You might think the system simply compares your (the user’s) geographical coordinates with those of drivers. But this approach requires scanning the coordinates of all drivers in the database to then find the ones around you.

And scanning each of those coordinates is a two-dimensional search because geographical coordinates consist of latitudes/longitude pairs.

So the database has to check both axes separately, which further slows down the operation. Why? Because most databases can only handle 1-dimensional data. Pretty complex and time-consuming, I know.

That’s the problem Gustavo Niemeyer noticed back in 2008 and presented the geohashing algorithm.

Geohashing takes a 2D pair of coordinates and turns them into a short alphanumeric string called a geohash. Since this string is linear, databases have to query less data to find nearby points of a given point.

This isn’t the only benefit of geohashing. It offers a lot more, but not without introducing a few inefficiencies along the way.

Read this comprehensive guide on geohashing to explore the good and the bad about geohashing. But more especially, read this blog to learn how the algorithm works. I have explained and demonstrated the steps to give you a thorough understanding.

Let’s start.

How Geohashing Works

Below is the step-by-step process that explains exactly how geohashing works in detail.

Step 1: Convert Latitude/Longitude Coordinates to Binary

A coordinate system made of latitude and longitude ranges defines the boundaries of the planet.

The latitude ranges from –90° to +90°, and the longitude goes from –180° to +180°.

A combination of numbers from these two ranges can describe any point on Earth.

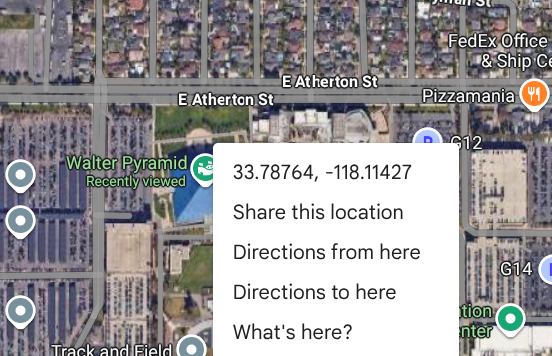
For instance, the (latitude, longitude) coordinates for the Walter Pyramid in California are 33.78764, -118.1142.

The geohashing algorithm splits in half the geographical coordinates of a location repeatedly to come up with the geohash string.

Each time the range is split in half, we record whether the coordinate falls in the upper or lower half.

• If your latitude is higher than the midpoint of –90° and +90°, we mark it as 1. 

• If it’s lower, it gets a 0.

The same logic applies to longitude. 

Bit by bit, this gives you two binary strings, one for latitude and one for longitude.

Now, the more we cut the ranges in half and record a binary bit, the longer the binary strings we get. And if we get longer strings, it means we get more precise locations.

Step 2: Interleave the Binary Latitude/Longitude Values

Next, the geohashing algorithm interleaves the two binary strings from the previous step. 

That means it takes one bit from longitude, then one from latitude, then one from longitude again. It keeps alternating like that until we have a single longer binary string. The first bit will always be the longitude bit.

This interleaving is what converts the two-dimensional data into one-dimensional data that databases can easily perform searches on.

Step 3: Convert Interleaved Binary String to Base32 String

Now this binary string is also very long and inefficient for both humans and machines.  

So geohashing compresses it into a shorter and more readable string using Base32 encoding.

For that, the binary string is split into 5-bit chunks. If your interleaved binary string is 20 bits long, you will have 4 5-bit chunks.

Then, the algorithm converts each 5-bit chunk into a single Base32 character using this alphabet:

• 0123456789bcdefghjkmnpqrstuvwxyz

Note: We skip the letters a, i, l, and o to avoid confusion with similar-looking digits like 1 and 0.

This conversion gives us an alphanumeric string, which we call a geohash. The length of this geohash determines the geohash precision:

• Fewer characters = a larger area (less precise)
• More characters = a smaller area (more precise)

Demonstration of the Steps

We’ve now gone through what is a geohash and how the geohashing algorithm works in theory. Now, it’s time to perform the steps on the geocodes of a location. 

How about I pick the coordinates of the Walter Pyramid (California) I mentioned before? 

Just to make you recall, its coordinates are 33.78764°, -118.1142°.

Step 1: Convert the Latitude Value (33.78764) Into a Binary String

We have the latitude value of 33.78764, and we know that latitude can range from -90 to +90.

We will start by comparing the midpoint of the initial range, [-90, +90], which is 0. Then, we will compare it with our latitude value.

By this comparison, we’ll find whether our latitude lies in the upper or lower half of the range [-90, +90].

If our latitude lies in the upper half (meaning it is greater than the midpoint)? We add the digit 1 to our binary string, and shorten the range accordingly. Otherwise, we get the digit 0.

So let’s start.

Iteration no.	Initial range	Midpoint	Latitude vs Midpoint	Binary digit	New range
1	[-90, +90]	0	33.78764 > 0	1	[0, +90]
2	[0, +90]	45	33.78764 < 45	0	[0, 45]
3	[0, 45]	22.5	33.78764 > 22.5	1	[22.5, 45]
4	[22.5, 45]	33.75	33.78764 > 33.75	1	[33.75, 45]
5	[33.75, 45]	39.375	33.78764 < 39.375	0	[33.75, 39.375]
6	[33.75, 39.375]	36.5625	33.78764 < 36.5625	0	[33.75, 36.5625]

I performed 6 iterations for the sake of this demo. The values of the Binary digit column will form our binary string for the latitude.

After ten iterations, our latitude binary string will be 1011000000. You can perform more or fewer iterations based on the level of precision you need.

Step 2: Convert the Longitude Value (-118.1142) Into a Binary String

Now, let’s repeat the same steps for our longitude value -118.1142.

A longitude value can range from [-180, +180], so that will be our initial range.

Iteration no.	Initial range	Midpoint	Longitude vs Midpoint	Binary digit	New range
1	[-180, 180]	0	-118.1142 < 0	0	[-180, 0]
2	[-180, 0]	-90	-118.1142 < -90	0	[-180, -90]
3	[-180, -90]	-135	-118.1142 > -135	1	[-135, -90]
4	[-135, -90]	-112.5	-118.1142 < -112.5	0	[-135, -112.5]
5	[-135, -112.5]	-123.75	-118.1142 > -123.75	1	[-123.75, -112.5]
6	[-123.75, -112.5]	-118.125	-118.1142 > -118.125	1	[-118.125, -112.5]

After ten iterations, our binary string for longitude will be 0010110000.

Step 3: Interleave the Latitude and Longitude Binary Strings

This is the easy step. We will interleave the latitude and longitude strings to form a single string.

We simply need to alternate one bit from longitude, then one from latitude, and so on.

The pattern is lon₁, lat₁, lon₂, lat₂, lon₃, lat₃, …

The first bit will always be the longitude bit.

• Our longitude is: 0010110000
• Our latitude is: 1011000000

The resulting 20-bit interleaved sequence will be:

• 10001110010100000000

Step 4: Convert Interleaved Binary String to Base32 String

Lastly, we’ll make 5-bit chunks of our interleaved string for Base32 encoding:

5-bit Group	Calculation	Decimal Value	Base32 Char
10001	(16 + 0 + 0 + 0 + 1)	17	j
11001	(16 + 8 + 0 + 0 + 1)	25	t
01010	(0 + 8 + 0 + 2 + 0)	10	b
00000	(0)	0	0

After putting the Base32 characters together, we finally get our geohash: jtb0.

So the geohash for the coordinates 33.78764°, -118.1142° is jtb0.

Geohashing Precision

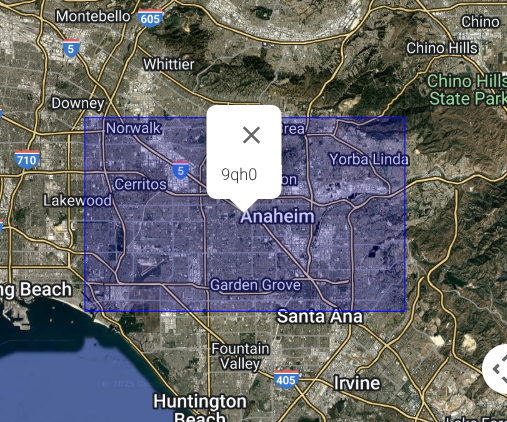
You can control the precision of a geohash by adding or removing a number from it.

When you add a character to its end, the location narrows down to a smaller area. And when you delete a character from its ending, the resulting geohash points to a broader region.

For instance, the image above shows how much area a 4-character-long geohash, 9qh0, represents.

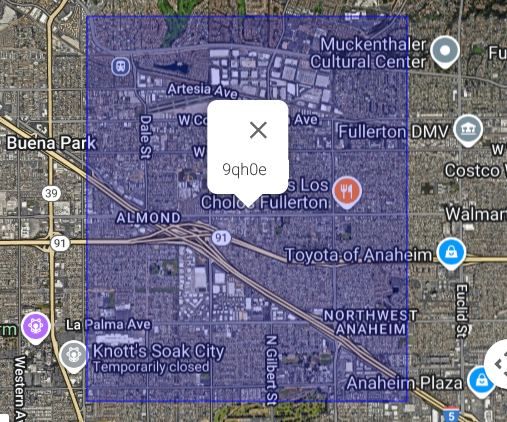
Increasing the precision of the same geohash to 5 characters zooms into the Anaheim city (see the image below).

Here’s a general idea of how geohash precision works as the code length increases:

• 1 character: ~Continent-sized area
• 2 characters: ~Region about the size of Western Europe
• 3 characters: ~Size of a city
• 4 characters: ~A district or neighborhood
• 5 characters: ~A town
• 6 characters: ~A city block
• 7 characters: ~Street or large building
• 8 characters: ~A building or parcel of land
• 9 characters: ~A specific part of a parking lot

Reasons To Use Geohashing

Here are two main reasons to use geohashing.

• Faster proximity searches: Geohashes free you from depending on heavy latitude and longitude ranges for performing proximity searches. The geographic neighbors of a geohash have similar prefixes, making it easy to compare the prefixes to find nearby points.
• Efficient database indexing: Geohashes don’t contain decimal floating points because, unlike latitude and longitudes, they’re strings. It makes them efficient for your standard database, which is good at handling strings.

Where Geohashing Is Used

Geohashing sees a huge usage in modern location-based services. 

Here are two of its major applications:

• Geospatial databases: Many databases use geohashing to handle location-based queries for spatial indexing. With this kind of spatial indexing, queries like “find all points within a radius” run faster than traditional 2D searches.

• Ridesharing and food delivery platforms: All ridesharing apps you have used to date have geohashing under the hood. The apps use geohashing to group drivers and riders into spatial buckets based on their current location. When you request a ride, the system looks for riders in the same or neighboring geohash cells. The same goes for food delivery apps. Instead of riders, they fetch all restaurants near your geohash cell.

Advantages of Geohashing

Some benefits that geohashing offers include:

• Hierarchical zooming: You can zoom in or zoom out of a map just by adjusting the number of characters in a geohash. To zoom in, you need to add a valid character to the geohash string. To zoom out, simply remove trailing characters to make the geohash shorter. 

• Built for scale: Geohashing optimizes both storage and query speed. Why? Well, because nearby locations share common prefixes, it makes it easy to shard data across servers.

• Database agnostic flexibility: Geohashes are compatible with any database that supports string indexing, and there are many of them. PostgreSQL, MySQL, and MongoDB are just a few examples.
• Compact and storage-efficient: Storing and sharing row floating point coordinates takes up more storage and space than short alphanumeric strings. This is why geohashes are ideal for APIs, URLs, and social media.

Disadvantages of Geohashing

While geohashing offers solutions for some big inefficiencies, it brings its fair share of limitations, like all algorithms.

• Uneven spatial distribution: The geohashing algorithm divides the world into rectangular grids, but this doesn’t perfectly match Earth’s curved and elliptical surface. This causes uneven spatial distribution, especially near the poles. For instance, when the latitude increases, geohash cells distort in size and result in slightly skewed proximity calculations. 
• Rigid grid boundaries: Let’s say two nearby points are lying on opposite sides of a boundary connecting two rectangular cells. When you run a proximity-based query on any one of these points, you overlook the nearby point in the adjacent cell. Simply because it isn’t in the same cell.

Alternatives to Geohashing

Geohashing isn’t the only method for spatial indexing. There are other popular systems as well.

Quadtrees / K-d Trees

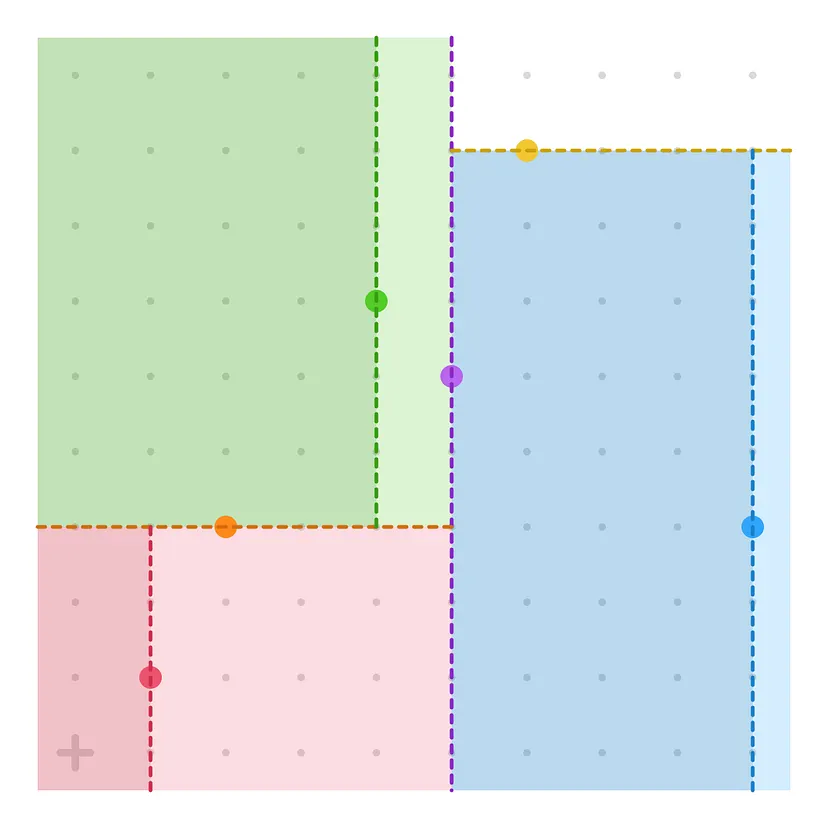
A Quadtree is a tree data structure that partitions a two-dimensional space by recursively subdividing it into four quadrants. 

It mainly differs from geohashing due to conditional subdivision. In geohashing, we divide the world into a fixed grid.

But in quadtrees, we divide a space based on a specific rule. For instance, we subdivide areas with more data.

In the real world, this dynamic subdivision helps in cases of biomes where high precision isn’t needed, like deserts/oceans.

The K-d tree data structure, on the other hand, performs recursive binary space partitioning along alternating axes.

K-d trees also adapt to data density, similar to quadtrees.

R-trees

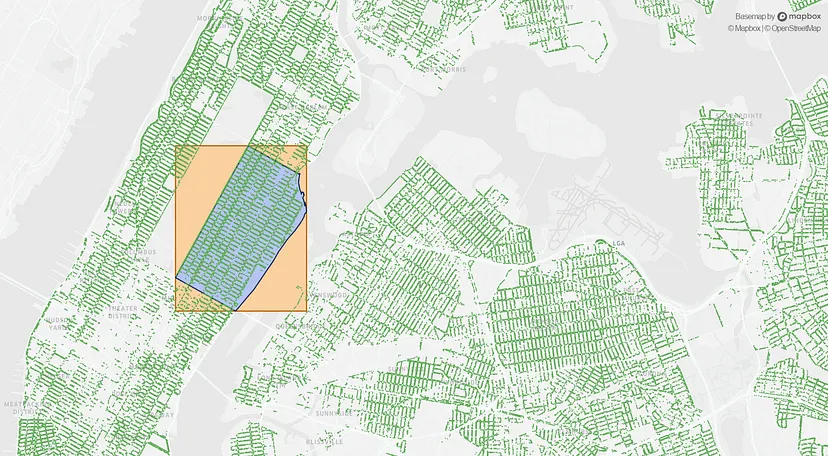
R-trees start from the bottom.

It groups nearby geographic objects like cities, rivers, and parks by drawing the smallest possible box around them.

Then, it nests these boxes inside larger boxes that represent the larger area around the smaller boxes.

Since R-trees work on the object level, their boxes can be of arbitrary shapes and sizes.

S2 Geometry

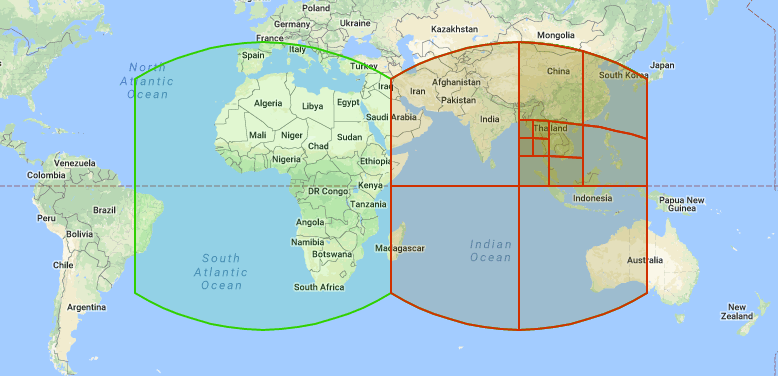
Google’s S2 Geometry places the earth inside a circumscribed cube. The sphere touches the cube at the center of each face.

Then, it performs a gnomonic projection. In simple words, this projects every point on the Earth’s surface radially outward onto the cube’s faces.

This creates a hierarchy of cells that cover the globe with minimal distortion.

S2 geometry then uses quadtrees to subdivide each face of the cube.

The Bottom Line

Geohashing offers a great way to turn 2D data into linear data for easy and, most importantly, hassle-free querying. While it has some issues like the edge case inaccuracy, it still sees popular usage in mainstream applications.

Besides geohashing, we also explored other alternatives that subdivide the world in their own ways.

Speaking of geography, GeoPlugin is a geolocation tool that can determine geographical details based on IP addresses. 

Website owners can use this to segment their visitors and dynamically change their website’s UI to offer personalized experiences.

Explore GeoPlugin to start geolocating IPs with our API.

FAQs